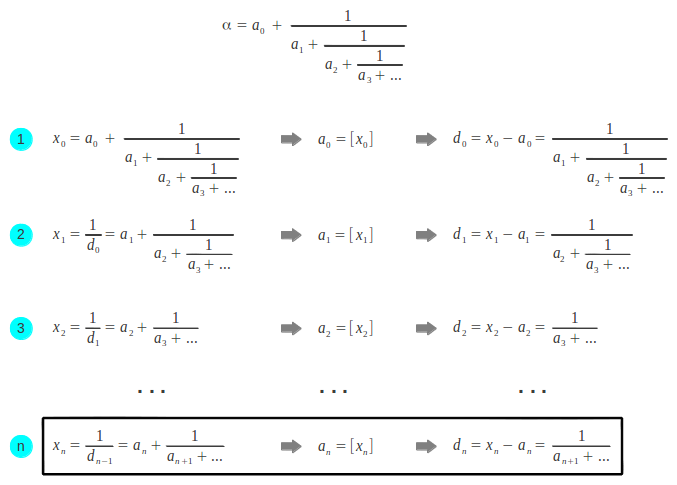
"Los fenómenos naturales se expresan a través del número sin que sea necesario medir.
La observación y la medida tan sólo consiguen verificar lo que ya estaba presente dentro del propio número.
Sólo podemos averiguar los secretos del número sujetándolo bajo la luz de la forma adecuada".
Jay Kappraff
La observación y la medida tan sólo consiguen verificar lo que ya estaba presente dentro del propio número.
Sólo podemos averiguar los secretos del número sujetándolo bajo la luz de la forma adecuada".
Jay Kappraff
Tabla de Contenido
1.- Introducción2.- Definiciones básicas
3.- Cálculo de los índices
4.- Cálculo de los convergentes
5.- Un procedimiento gráfico: el árbol de Farey
6.- Fracciones continuas de números irracionales
7.- Números nobles
8.- Referencias
Apéndice
1.- Introducción
Más allá de los números enteros, encontramos las fracciones -también conocidas como números racionales- que expresan una relación entre dos cantidades enteras (dos lados de un polígono, las frecuencias de dos osciladores, etc.). Cuando los escribimos en notación decimal, o bien tienen un número finito de cifras decimales, como 235/100=0.235, o un número infinito de decimales repetitivos, como 11/7=1.571428571428571428... La otra "mitad" de la película está protagonizada por los números irracionales, aquellos con una secuencia de decimales infinita y no repetitiva. Algunos de ellos, como φ=1.6180339887... o π=3.1415926535... desempeñan un papel clave en la Geometría Sagrada.El objetivo de este artículo es proporcionar una herramienta, las fracciones continas, mediante la cual se puede analizar y extraer la estructura interna de cualquier número real, ya sea racional o irracional. Las fracciones continuas nos permiten comprender por qué, entre el infinito número de secuencias que convergen a la Razón Aurea φ, la secuencia de Fibonacci es tan especial; o qué significa que la Proporción Aurea sea el número más irracional; o por qué algunos irracionales especiales, conocidos como Números nobles y muy relacionados con φ, juegan un papel clave en muchos fenómenos naturales como la filotaxis de las plantas. Por el camino emergerá de forma natural una jerarquía de racionales conocida como el árbol de Farey, con muchas implicaciones en física y química.
2.- Definición básica
Vamos a coger como ejemplo la fracción 5/12. Este número también se puede expresar de la siguiente forma alternativa: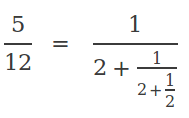
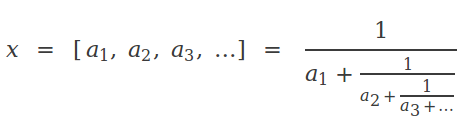
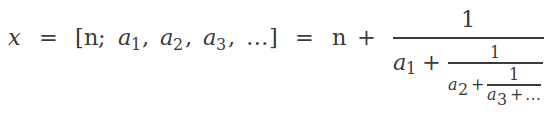
3.- Cálculo de los índices
Veamos cómo podemos calcular los índices de la fracción continua de un número dado. Primero vamos a focalizarnos en los racionales. Consideremos un número racional expresado como una fracción A/B. El punto clave aquí es darse cuenta de que, si lo invertimos B/A, su parte entera es el primer índice a1. Así pues a1se puede obtener por una simple división entera. Para obtener los índices restantes, tan sólo necesitamos iterar el proceso usando el resto como nuevo divisor, tal como se muestra a continuación:
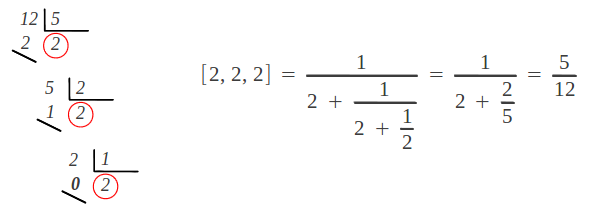
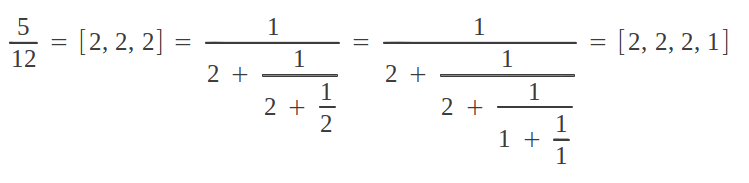
4.- Cálculo de los convergentes
Truncando la fracción continua de un número x = A/B en puntos sucesivos de su desarrollo, obtenemos aproximaciones racionales Pk/Qk de x denominadas sus convergentes: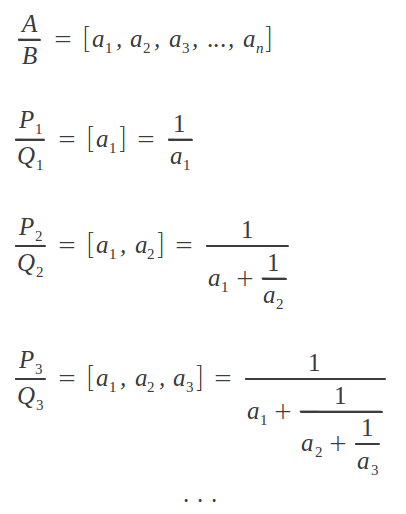
A medida que añadimos más índices al convergente, su cálculo directo se vuelve más y más complicado. Sin embargo, existe un método iterativo que nos permite calcular un convergente dado a partir de los dos precedentes [Kapp]. Para inicializar el proceso necesitamos calcular P1/Q1, para el cual no existen convergentes previos; en este caso asumimos las condiciones iniciales P-1/Q-1 = 1/0 y P0/Q0=0/1. El proceso a seguir puede expresarse en forma de tabla como sigue:


5.- Un método gráfico: el árbol de Farey
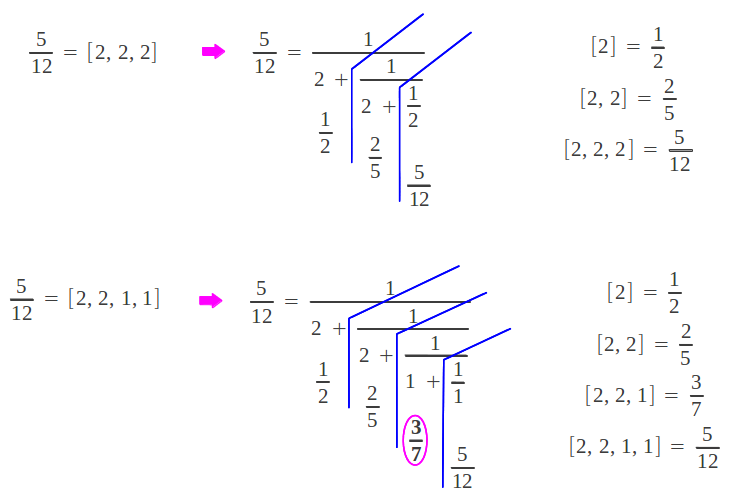
Hasta el momento hemos aprendido cómo obtener los índices de la fracción continua de un número racional dado, y cómo calcular sus convergentes a partir de esos índices. El lector se puede estar preguntando: ¿existe alguna forma más sencilla de calcular la fracción continua de un número racional? Pues resulta que sí: existe un método gráfico que permite "ordenar" de alguna forma los números racionales y calcular fácilmente la expansión en fracción continua de un número racional dado. La fracción continua más simple (y corta) después de la unidad [1] = 1/1 es claramente [1,1] = [2] = 1/2. Un número racional cercano se puede obtener a través de lo que se conoce como "mediana" entre estos dos números racionales, que consiste en calcular una nueva fracción resultante de sumar numeradores y denominadores por separado, tal como se ilustra a continuación: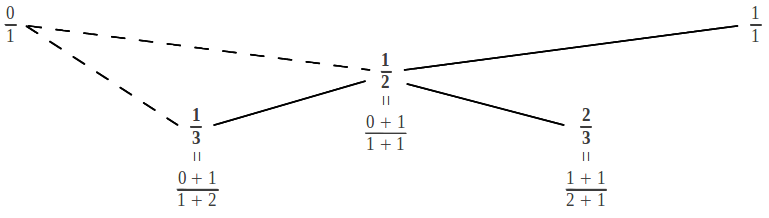
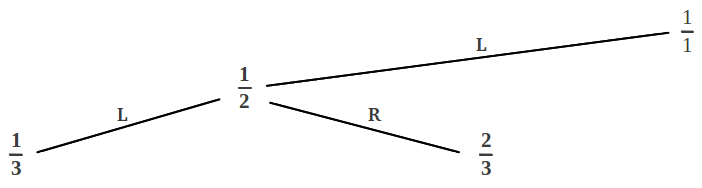
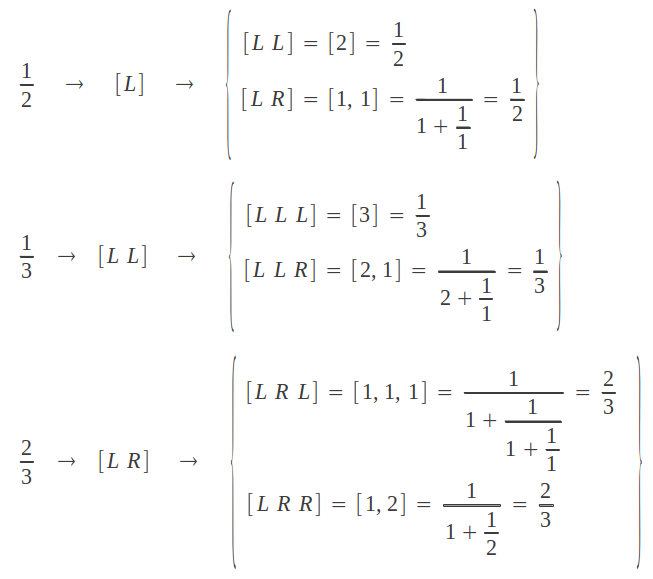
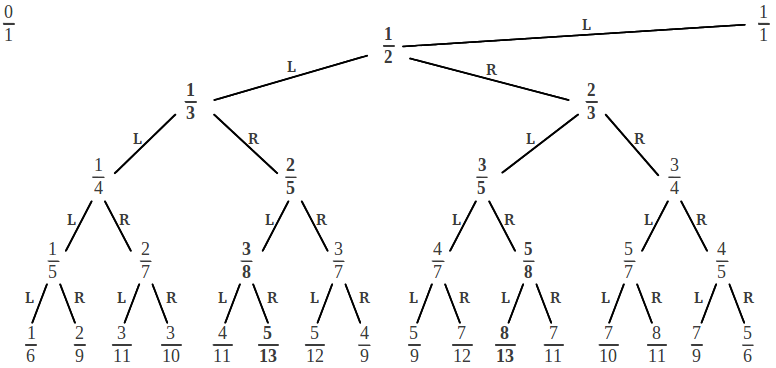
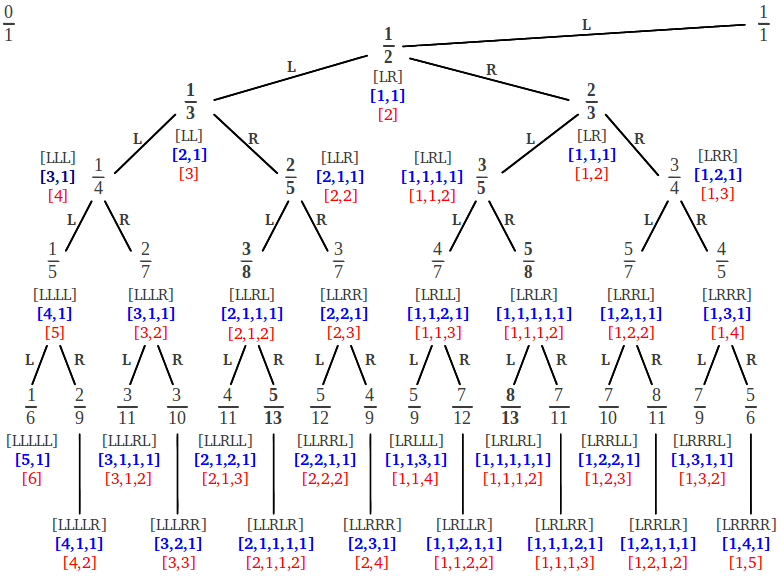
(1) La secuencia de pasos L-R que conducen a un número racional dado, añadiéndole una R o una L final, proporciona las dos fracciones continuas equivalentes de este racional: la "compacta" y la "extendida". Por ejemplo para alcanzar 5/12 seguimos la secuencia de pasos[LLRRL]. Si completamos esta secuencia con una L final, obtenemos [LLRRLL] = [2, 2, 2]; por el contrario, si la completamos con una R final, obtenemos [LLRRLR] = [2, 2, 1, 1].
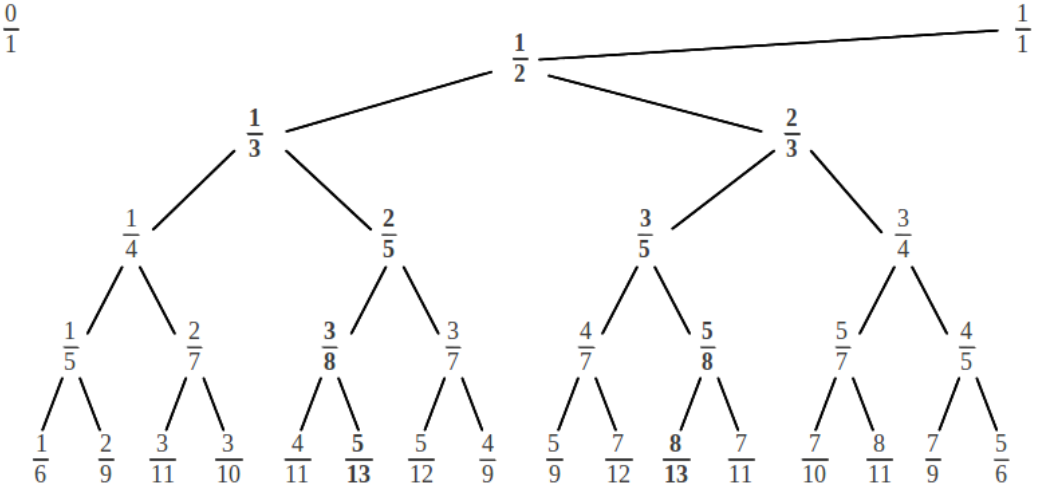
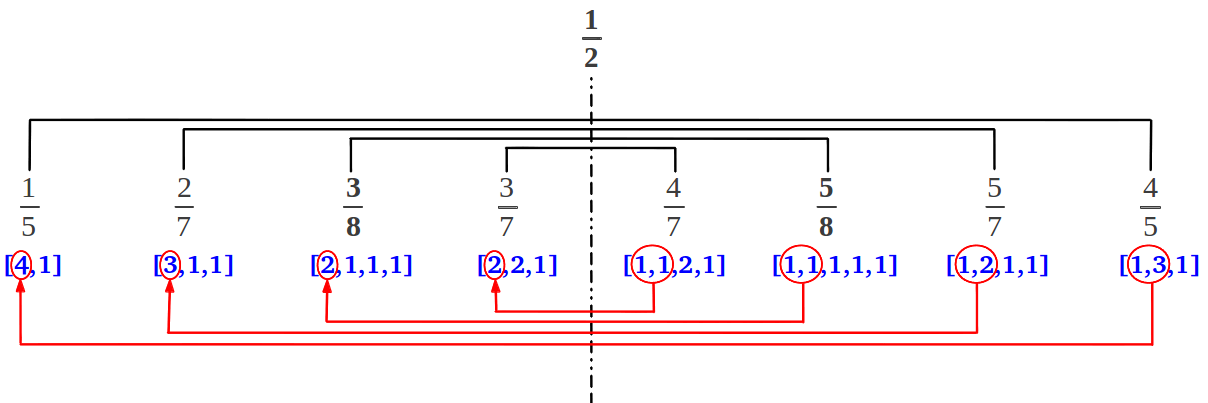
(2) Cualquier nueva fila del árbol de Farey contiene el doble de fracciones que la fila precedente, porque se introduce un nuevo elemento entre cada par existente. Además, cada fila tiene simetría especular: si trazamos una vertical de 1/2 hacia abajo, a cada lado de esta línea encontramos una pareja de fracciones complementarias que suman 1. Por ejemplo, en la tercera fila, encontramos las parejas 3/7 y 4/7, 3/8 y 5/8, 2/7 y 5/7, y 1/5 y 4/5. Es más, basta conocer la fracción continua de los elementos ubicados a la derecha de 1/2: la fracción continua de sus complementarios es la misma pero con las dos cifras de más a la izquierda sumadas, como se muestra a continuación:
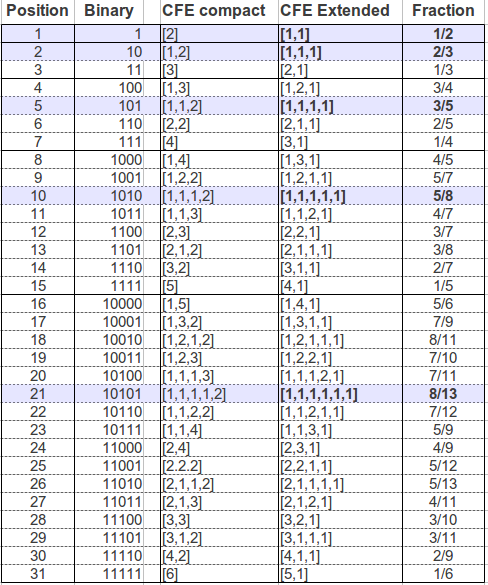
También resulta interesante observar que a cada número racional de la tabla anterior se le ha asignado una posición absoluta, un número natural. El lector puede comprobar que esta posición puede obtenerse a partir del árbol de Farey numerando los racionales de cada fila de derecha a izquierda, empezando por la primera fila (1/2) y procediendo hacia abajo. El hecho clave es que esos números de posición no son arbitrarios: cada uno de ellos está directamente relacionado con la representación en fracción continua del correspondiente racional. Por ejemplo, imagínese que quisiéramos saber cual es el 25º racional del árbol. Para conseguirlo sólo tenemos que escribir 25 en notación binaria, 25 = 11001, y sustituir cada 1 por un paso L y cada 0 por un paso R. El resultado final es [LLRRL] que después de completarse con una L o una R da lugar a [2, 2, 2] = [2, 2, 1, 1] = 5/12. Así pues, según este proceso existe un número racional asociado a cada número natural.
6.- Fracciones continuas de números irracionales
Hasta ahora nos hemos centrado en los números racionales, pero ¿qué pasa con los irracionales? Tal como hemos comentado más arriba, la expansión en fracción continua de un número irracional α tiene un número infinito de índices. Esta epansión también se puede truncar en pasos sucesivos, dando lugar a los convergentes Pk/Qk del número irracional α. Existe un procedimiento general para calcular la representación en fracción continua de cualquier número irracional, siempre que conozcamos su representación decimal exacta (véase el Apéndice). Algunos ejemplos de fracciones continuas de números irracionales notables son los siguientes [Barr]:
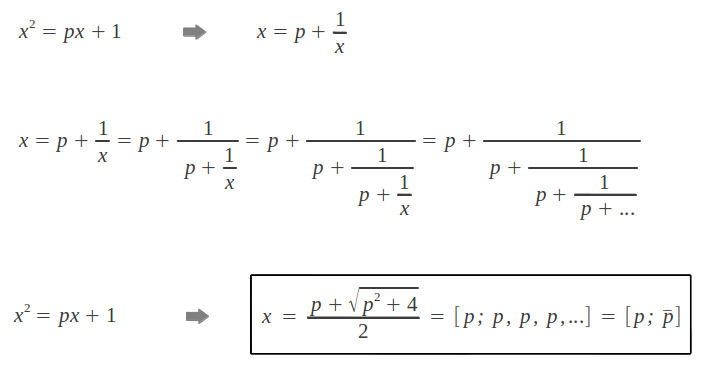
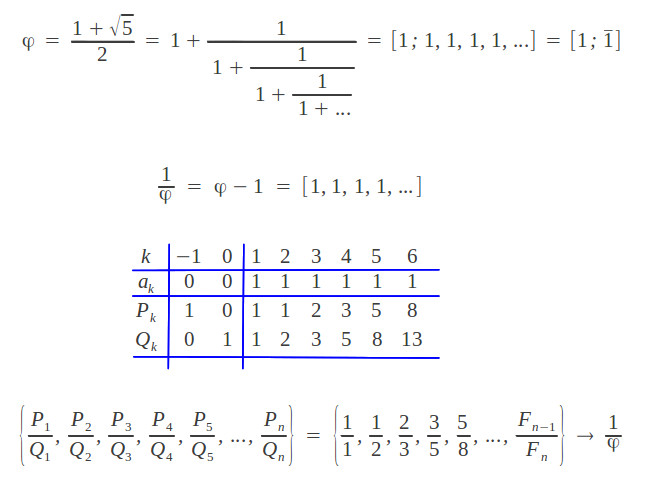
Ahora también estamos en posición de comprender por qué la Proporción Aurea es el número más irracional. La respuesta está directamente relacionada con el grado con el que se puede aproximar sucesivamente un número racional α a partir de los convergentes Pk/Qk de su expansión en fracción continua. Una medida de la aproximación de Pk/Qk a α viene dada por [Kapp]:
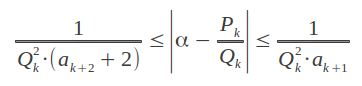
Ahora consideremos α = 1/φ en la desigualdad previa. Como todos los índices de su descomposición en fracción continua son igual a 1, se trata del número irracional con la peor aproximación a sus convergentes. Y como los convergentes son la mejor aproximación racional a su número límite irracional, 1/φ es el número irracional que se encuentra más lejos de los racionales que cualquier otro numero irracional -que necesariamente tendrá una descomposición en fracción continua con índices mayores que uno.
7.- Números Nobles
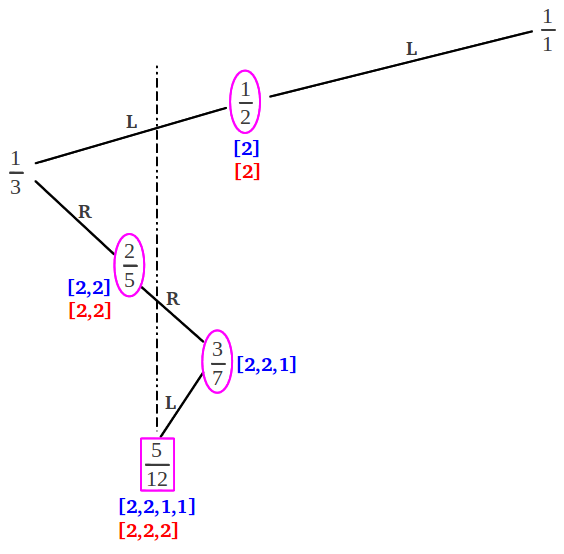
Cualquier número irracional comprendido entre 0 y 1 cuya expansión en fracción continua sea de la forma τG = [a1, a2, ..., an, 1, 1, 1, ...], donde ak≥1, se denomina Número Noble. El número más noble de todos es el inverso de la Proporción Aurea 1/φ = [1, 1, 1, 1, ...]. El siguiente Número Noble en importancia es 1/φ2 = [2,1,1,1,...]. Resulta muy instructivo observar donde se encuentran los convergentes de estos números dentro del árbol de Farey. Tal como hemos mencionado más arriba, una fracción continua con una secuencia finita de unos corresponde a números racionales que descienden en zigzag por el árbol de Farey siguiendo los pasos [LRLR ...] = [1,1,1,1, ...]. El inverso de la Proporción Aurea empieza a hacer zigzag desde el principio. Cualquier otro Número Noble empieza el zigzag más adelante, después de un determinado número finito de pasos por el árbol que no siguen exactamente una secuencia L-R. A partir de un número racional dado, por ejemplo 5/12, existen dos formas de descender haciendo zigzag: o bien a partir de la fracción situada inmediatamente encima y a la derecha de 5/12, en este caso 3/7; o bien a partir de la fracción situada inmediatamente encima y a su izquierda, es decir 2/5: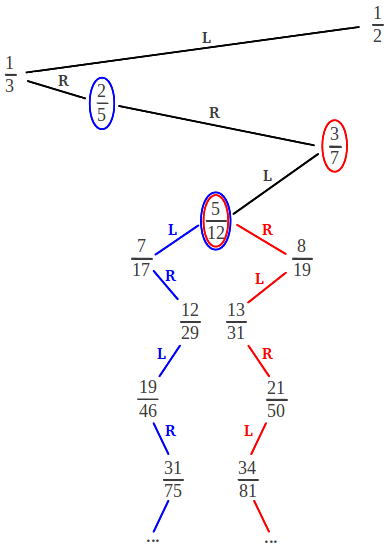
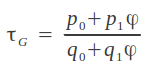
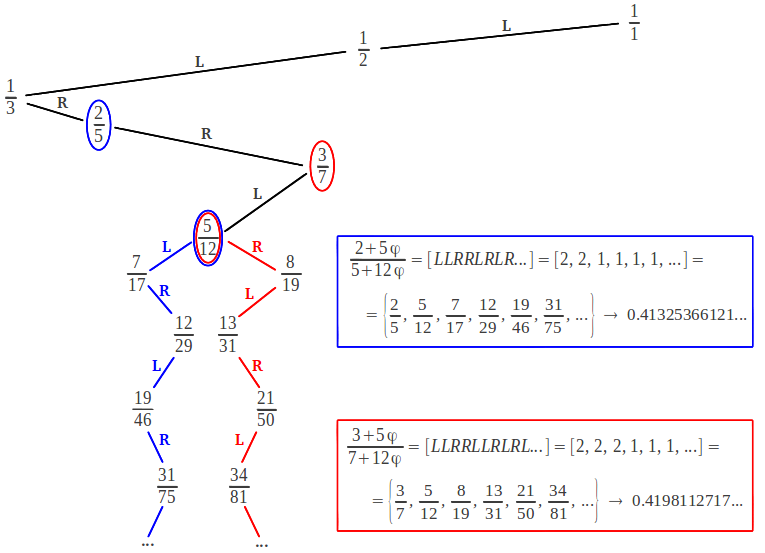
Los Números Nobles también comparten con la Proporción Aurea la propiedad de ser los números "más irracionales", debido a la cola de 1's en su expansión en fracción continua. Estas dos propiedades explican, por un lado, su presencia en el estudio de la filotaxis de las plantas. Citamos textualmente a Jay Kappraff [Kapp, p. 325]: "Cuando los Números Nobles se multiplican por 360 grados, propocionan unos ángulos especiales relacionados con el crecimiento de las plantas que se conocen como ángulos de divergencia. Estos ángulos describen la ubicación de las cabezuelas en la superficie de una planta, como las que dan lugar a los giros en espiral de un girasol. Por ejemplo el irracional [2,1,1,1,...] = 1/φ2 es el número más prevalente, y conduce al ángulo 360/φ2 = 137.5 grados. El siguiente ángulo más importante es [3,1,1,1,...] el cual, cuando se multiplica por 360 da lugar a 99.5 grados. El siguiente ángulo en importancia es [2,2,1,1,1,...] y da lugar a 151.1 grados".
El hecho de que los Números Nobles sean los que peor se pueden aproximar por cualquier número racional también los hace importantes en muchos problemas de órbitas caóticas de la física. John D. Barrow lo explica de una forma muy elegante [Barr]: "Estos números caracterizan las frecuencias de aquellos movimientos ondulatorios que son los menos susceptibles de ser perturbados hacia una inestabilidad caótica. Típicamente, un sistema que puede oscilar de dos formas, como una estrella que está orbitando alrededor de una galaxia y también está bamboleandose por encima y por debajo del plano de la galaxia, tiene dos frecuencias que determinan estas oscilaciones distintas. Si el cociente de esas dos frecuencias es una fracción racional, entonces en última instancia el movimiento será periódico, pero si se trata de un número irracional entonces el movimiento será no periódico, explorando todas las posibilidades compatibles con la conservación de su energía y su momento angular. Si perturbamos un sistema que tiene un cociente de frecuencias racional, éste puede ser fácilmente desplazado a una situación caótica con frecuencias irracionales. La Proporción Aurea es la más estable porque está siempre lejos de uno de esos cocientes racionales. De hecho, la estabilidad de nuestro sistema solar durante largos períodos de tiempo está supeditada a determinados cocientes de frecuencias muy cercanos a Números Nobles".
8.- Referencias
[Kapp] Kappraff, Jay: "Beyond Measure: a guided tour through Nature, Myth and Number", World Scientific Publishing, 2002.[Barr] Barrow, John D: "Chaos in numberland: The secret life of continued fractions", Plus Magazine, 2000.
Apéndice: Cálculo de la fracción continua de un número real
Excepto en algunos casos particulares que hemos explorado en las secciones previas, en general para calcular la fracción continua de un número irracional necesitamos conocer su representación decimal. Si este es el caso, entonces podemos seguir un proceso parecido al de la Sección 4, pero para obtener los "cocientes" de una división real necesitamos tomar la parte entera del resultado. Vamos a denotar la parte entera de un número α como [α]. El proceso general es el siguiente: si el número α es mayor que 1, entonces extraemos su parte entera a0 = [α]. Para obtener el primer índice del denominador, a1, sólo necesitamos invertir el número y tomar su parte entera. Luego este proceso de invertir y tomar la parte entera puede iterarse tantas veces como sea necesario: